极坐标下的面积

马同学

极坐标下的面积

1 曲边扇形

定义 .由 $\rho=\rho(\theta)$ 及两条射线 $\theta=\alpha$ 、 $\theta=\beta$ 所围成图形称为曲边扇形。

下图所示的就是某曲边扇形。

2 极坐标下的面积

定义 .若极坐标函数 $\rho=\rho(\theta)$ 在区间 $[\alpha,\beta]$ 上连续，且有：
$\rho(\theta)\geq 0\quad 0 < \beta-\alpha \leq 2\pi$
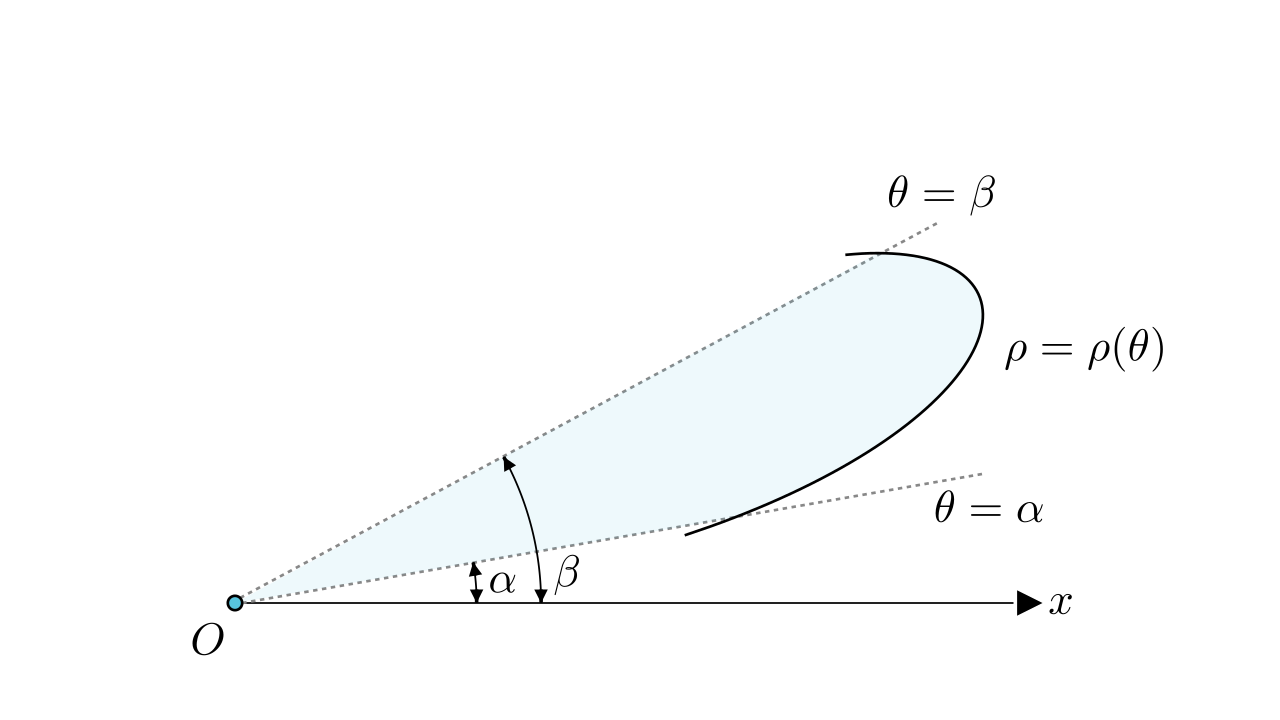
则定义由 $\rho=\rho(\theta)$ 及两条射线 $\theta=\alpha$ 、 $\theta=\beta$ 所围成的曲边扇形的面积 $A$ 为：
$A=\lim_{\lambda\to 0}\sum_{i=1}^{n}\frac{1}{2}[\rho(\xi_i)]^2\Delta\theta_i=\int_{\alpha}^{\beta}\frac{1}{2}\left[\rho(\theta)\right]^2\mathrm{d}\theta$

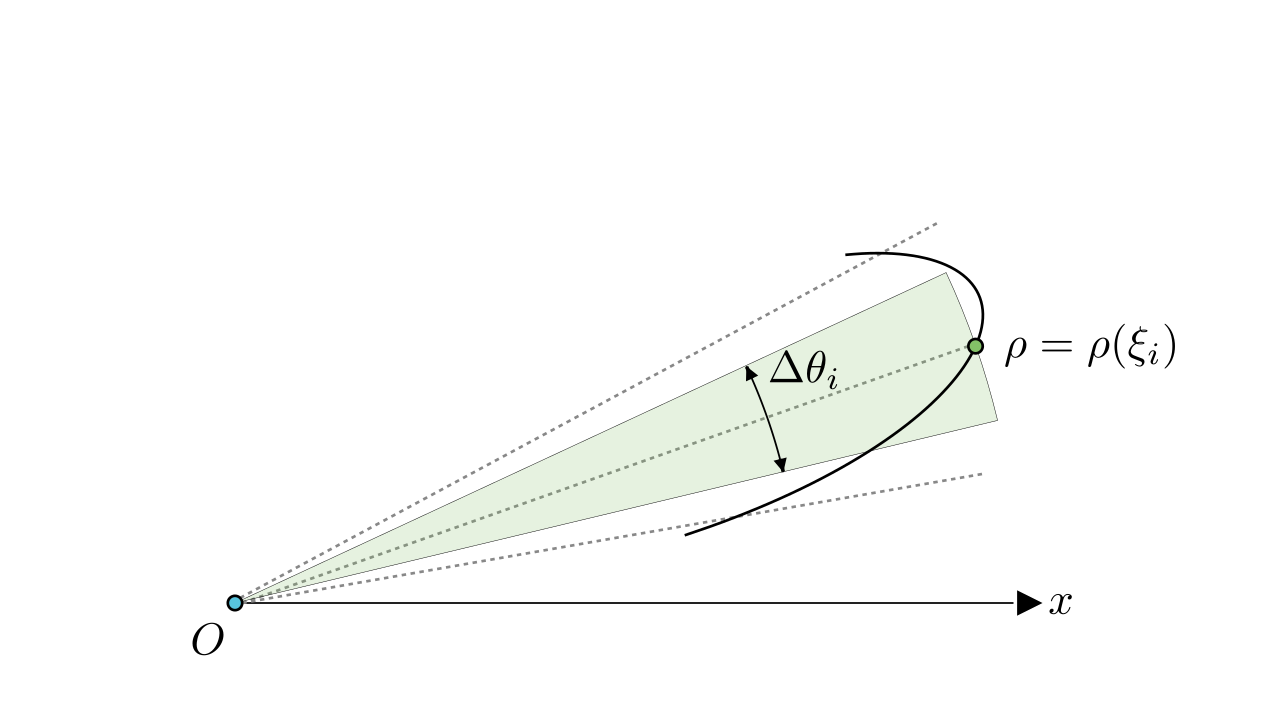
下面通过一个例子来解释一下上述定义。也是和曲边梯形的面积类似，我们可以通过小扇形的面积和来计算曲边扇形的面积，如下图所示。

让我们观察下其中的小扇形。把区间 $[\alpha,\beta]$ 任意分为 $n$ 份，其中某子区间 $[\theta_{i-1}, \theta_i]$ 的角度差为 $\Delta\theta_i=\theta_i-\theta_{i-1}$ ，作半径为 $\rho(\xi_i)$ （ $\xi_i\in[x_{i-1},x_i]$ ）中心角为 $\Delta\theta_i$ 的小扇形，如下图所示。

根据高中几何知识，可知该小扇形的面积为 $\frac{1}{2}\left[\rho(\xi_i)\right]^2\Delta\theta_i$ ，所以在区间 $[\alpha,\beta]$ 上 $n$ 个小扇形的面积和为如下黎曼和：

$\sum_{i=1}^{n}\frac{1}{2}\left[\rho(\xi_i)\right]^2\Delta\theta_i$

令 $\lambda=\max\{\Delta\theta_1,\Delta\theta_2,...,\Delta\theta_n\}$ ，因为极坐标函数 $\rho=\rho(\theta)$ 在区间 $[\alpha,\beta]$ 上连续，根据可积的充分条件 1，所以 $\lambda\to 0$ 时上述黎曼和的极限存在，也就是可积。所以定义由 $\rho=\rho(\theta)$ 及两条射线 $\theta=\alpha$ 、 $\theta=\beta$ 所围成的曲边扇形的面积 $A$ 为：

$A=\lim_{\lambda\to 0}\sum_{i=1}^{n}\frac{1}{2}[\rho(\xi_i)]^2\Delta\theta_i=\int_{\alpha}^{\beta}\frac{1}{2}\left[\rho(\theta)\right]^2\mathrm{d}\theta$

关注马同学

微信公众号：matongxue314

马同学机器学习

监督式学习(更新中)

适合机器学习零基础入门

马同学图解数学

关注马同学

微信公众号：matongxue314

极坐标下的面积

监督式学习(更新中)

线性代数(已完本)

单变量微积分(已完本)

多变量微积分(已完本)

概率与统计(已完本)