曲率
定义 .对于半径为的圆,
称为该圆的 曲率 (Curvature)。
圆的曲率是对圆的弯曲程度的描述。如下图所示,可以看到圆的半径越小的圆的弧越弯曲,也就是圆的曲率越大。

定理 .已知函数在
点有二阶导数
,且
,则此点有 曲率圆 (Osculating circle),也称为 密切圆 。
若用
表示该曲率圆的圆心,则
和
值为:
该曲率圆的半径
称为 曲率半径 ,其值为:
函数
在
点的 曲率 (Curvature)
定义为该曲率圆的曲率,即:
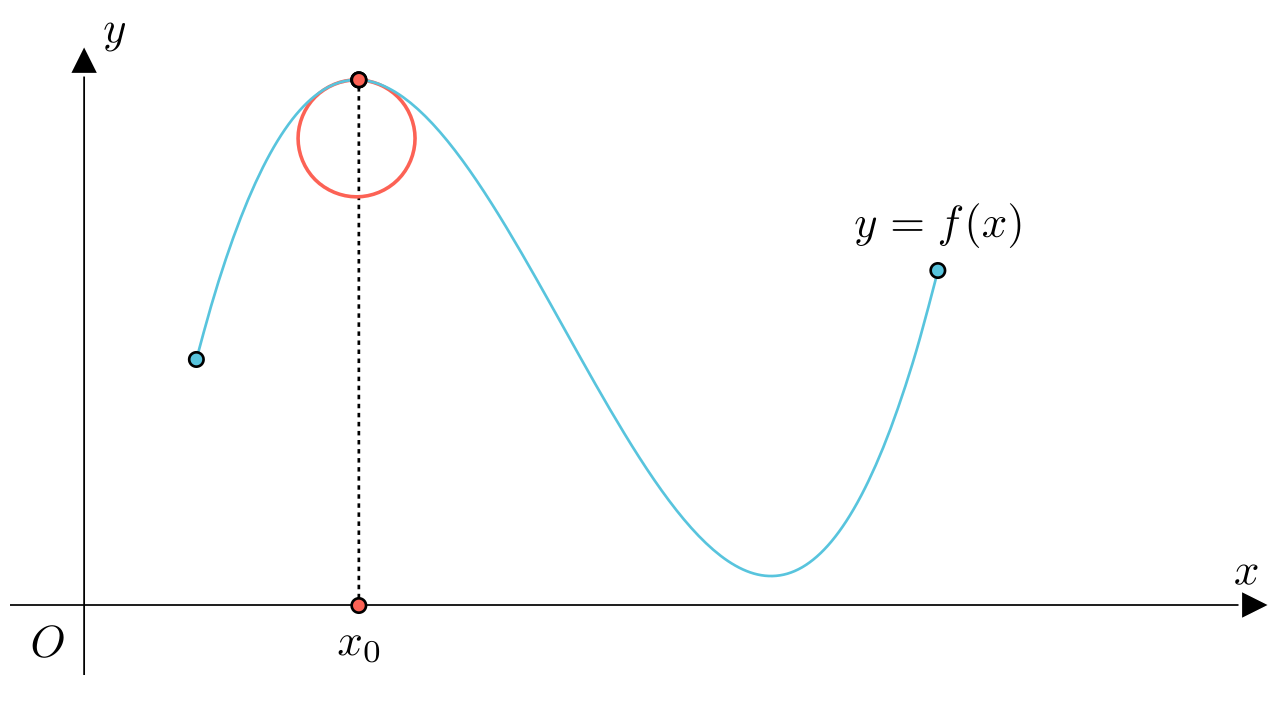
上述定理给出了曲率圆的定义,以及如何求出。所谓曲率圆就是可以逼近函数在
点附近曲线的圆,如下图所示。曲率圆的曲率也就是函数
在
点的曲率,描述了函数
在
点弯曲程度。
关注马同学

微信公众号:matongxue314




