马同学

如何理解线性微分方程？

线性微分方程为什么有“线性”这两个字？为什么线性微分方程的通解包含e^x？
刚开始学习线性微分方程的时候，我心中有两个疑问：
  • 线性微分方程为什么有“线性”这两个字？
  • 为什么线性微分方程的通解里面有？
这篇文章就来回答这两个问题。让我们从什么是线性变换开始。
1 线性变换
先直观感受一下什么是线性变换。
1.1 线性变换的几何意义
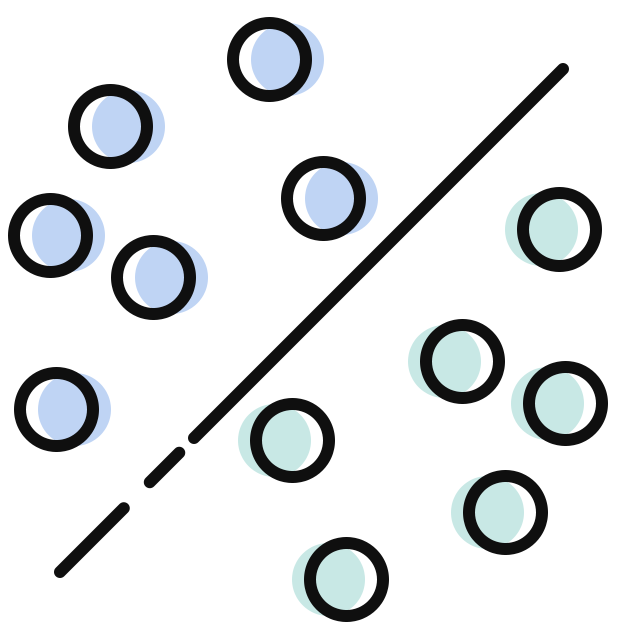
直观来说，线性变换就是把直线上的点（向量），变换到另外一根直线上去。关于这个问题更具体的解释，请参看文章如何理解相似矩阵的前半部分。
比如下图，把虚线上的点，变换到实线上去：
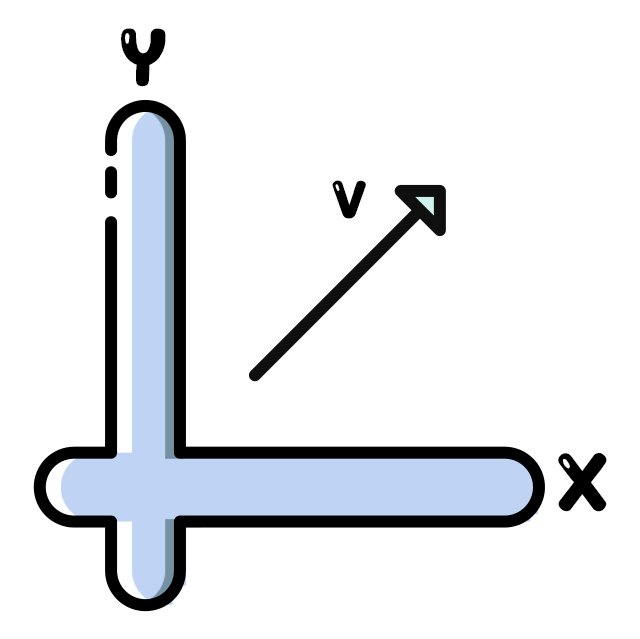
或者把整个二维平面上的直线换个位置（下面是一个镜面翻转，为了方便观察，标出一个，虚线表示翻转的对称轴）：
1.2 微分算子
我们来看一个不一样的向量，对于多项式函数：
我们以为基（关于多项式的基，可以参看《线性代数应该这样学》这样的高等代数教材），可以把它转为向量：
画出来图来就是（三个坐标轴分别表示这三个基，当然这里有点不严格，准确来说，三个基并不是两两正交的）：
我们定义为微分算子：
那么有：
还可以把写成一个矩阵（对于更高次的多项式，的矩阵是类似的）：
然后通过矩阵来完成求导操作：
从图像上看，就是把通过矩阵把投影到平面：
这样看来，微分算子也是一个线性变换。
1.3 代数定义
在数学中，只要符合下面两个性质的就是线性变换（代表变换)：
  • 可加性：
  • 齐次性：
上一节中，通过几何展示的线性变换都符合上述两个性质。
比如，我们有两个多项式函数：
那么容易验证，是一个线性变换：
  • 可加性：
  • 齐次性：
进一步的，的多项式组合：
也是线性变换，这一点可以自行去验证。
2 线性微分方程
既然的多项式组合是线性变换，那么线性微分方程为什么是“线性”的，答案呼之欲出。
2.1 线性微分方程的定义
定义下式为常系数（因为是常数）线性微分方程：
如果，，则为常系数齐次线性微分方程：
如果，，则为常系数非齐次线性微分方程：
如果是的函数，那么就是变系数线性微分方程。本文不讨论这种情况。
解释一下：
可以类比于齐次线性方程：
所以我们称为齐次线性微分方程。
不光是可以这么类比，实际上解法都是一样的。我们先来看看齐次线性方程是怎么解的。
2.2 齐次线性方程的解法
对于齐次线性方程：
我们怎么解？
我们知道，的特征值和特征向量满足下面这个等式：
那么特征值对应的特征向量必定是的解。
2.3 的特征值、特征向量
那么的特征值和特征向量是多少？
根据特征值和特征向量的定义，对于有：
所以，其特征值为，特征向量为。
啊哈，出现了，为什么线性微分方程的通解里面有，是因为是的特征向量啊。
同理，对于有：
所以，其特征值为，特征向量为。
2.4 解常系数齐次线性微分方程
万事具备，我们开始解方程吧。
对于：
实在太简单了，。
对于：
对于此，求它的0特征值：
对应的特征向量为，，这两个特征向量线性无关，因此得到解为：
如果得到的特征值相同，那么就需要另外讨论一下。
2.5 解常系数非齐次线性微分方程
对于非齐次线性微分方程：
可以类比线性方程的解的结构：
先求出齐次方程的解，然后根据初始条件得到一个特解，得到：
还有一种做法，因为：
所以可以得到：
得到一个新的齐次线性微分方程，然后根据刚才介绍的方法进行求解。不过这样就需要求解三次方程，或许比特解法复杂一些，这里只是展示一下理解了线性微分方程的含义之后，我们可以更灵活的处理。
3 总结
文章开头的两个问题，现在有了答案：
  • 因为是线性的，所以线性微分方程是线性的
  • 因为是的特征向量，所以通解里面有
关注马同学
马同学高等数学
微信公众号：matongxue314
马同学机器学习
马同学图解数学
马同学高等数学
微信公众号：matongxue314
©2021 成都十年灯教育科技有限公司 | 蜀ICP备16021378