我们在在《马同学图解微积分(上)》中介绍一元函数的积分学时，先是介绍了，如下图所示。

然后介绍了的面积可以通过来逼近，如下图所示，从而引入了。

类似的，也让我们从曲顶柱体的定义、体积计算开始，从而来引入多元函数的积分。

比如下图所示的就是一个曲顶柱体。

曲顶柱体的体积可以这样计算，先把均分成个，记作：

观察其中的第个小，如下图左侧所示。以该小的边界曲线为作平行于轴的，可得一个小的曲顶柱体，如下图右侧所示，显然该小曲顶柱体是大曲顶柱体的一部分。

由于顶面是的，因此上述小曲顶柱体的顶面起伏不大，所以可在小上任意选择一点作为点，比如像下图左侧一样选择的中心点作为点。以小为底、为高作一平顶柱体，去近似上述的小曲顶柱体，如下图右侧所示。容易算出该平顶柱体的体积小的面积也用来表示。

按照上述方法，作出所有以小为底、小中心点的函数值为高的小平顶柱体，就可以近似整个曲顶柱体，如下图所示。此时所有小平顶柱体的体积和为。

将均分成更多的小，即不断增加，这些小平顶柱体对曲顶柱体的近似效果越好，如下图所示。

所以可定义当时，这些小平顶柱体的体积和就是曲顶柱体的体积，即：

上一节介绍了的体积定义为，其更严格形式要由本节将要介绍的二重积分给出。

上述二重积分的定义简单来说就是，当满足下列两个要求时，

• 将任意分成个小，需要保证时有
• 任意选择点，需要保证点在小上

若下列极限存在，就称此极限为函数在上的二重积分，即：

这么说还是比较抽象，下面通过再次讨论的体积定义来理解一下上述二重积分的定义。

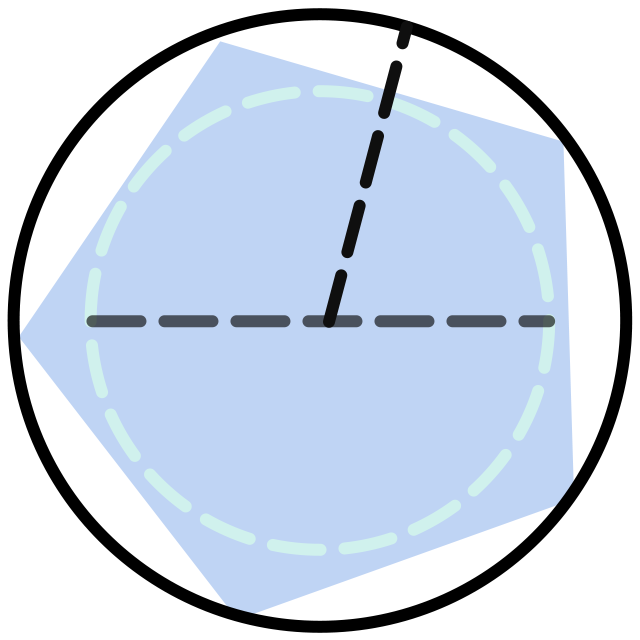
先解释下其中的“时有”。上一节给出的体积定义时，将方形进行了均分，每个都是同样的小正方形。因此在这里所有的最大直径就是其中某个的对角线，如下图左侧所示。随着增大，随之缩小，也随之缩小，如下图右侧所示。容易理解，这种划分方式可以保证时有。

除了上述的平均划分方式之外，根据二重积分的定义，我们还需要考虑所有可以保证时有的划分，比如下图的所示的两种不规则划分。

而如下图所示，虽然在不断增大，但由于其中红色的格子始终保持不变，所以并没有，这样的划分是不满足要求的。

再解释下其中的“任意选择点，需要保证点在小上”。除了像上一节那样选择的中心点作为点外，我们还需要考虑所有在小上的点都可以选为点，比如下图中的两种选取方式。

综上，考虑到任意划分、任意选取点，之前给出的体积定义需要修正为：

直观来说就是，任意划分、任意选取点，最终构成的这些小平顶柱体也是可以近似曲顶柱体的，如下图所示。

这里有一点需要解释，根据可知其顶面函数在上，可以证明，在这个条件下函数在上的二重积分必定存在类似于《马同学图解微积分·上》中学习过。所以不用考虑任意划分、任意选取点，只考虑均分、选择的中心点作为点的情况就可以了，所以定义的体积为也是正确的。

上面对进行图示时都是用的矩形，实际上也是存在非矩形的，如下图所示。二重积分的定义在非矩形上也是适用的，这里不再赘述。