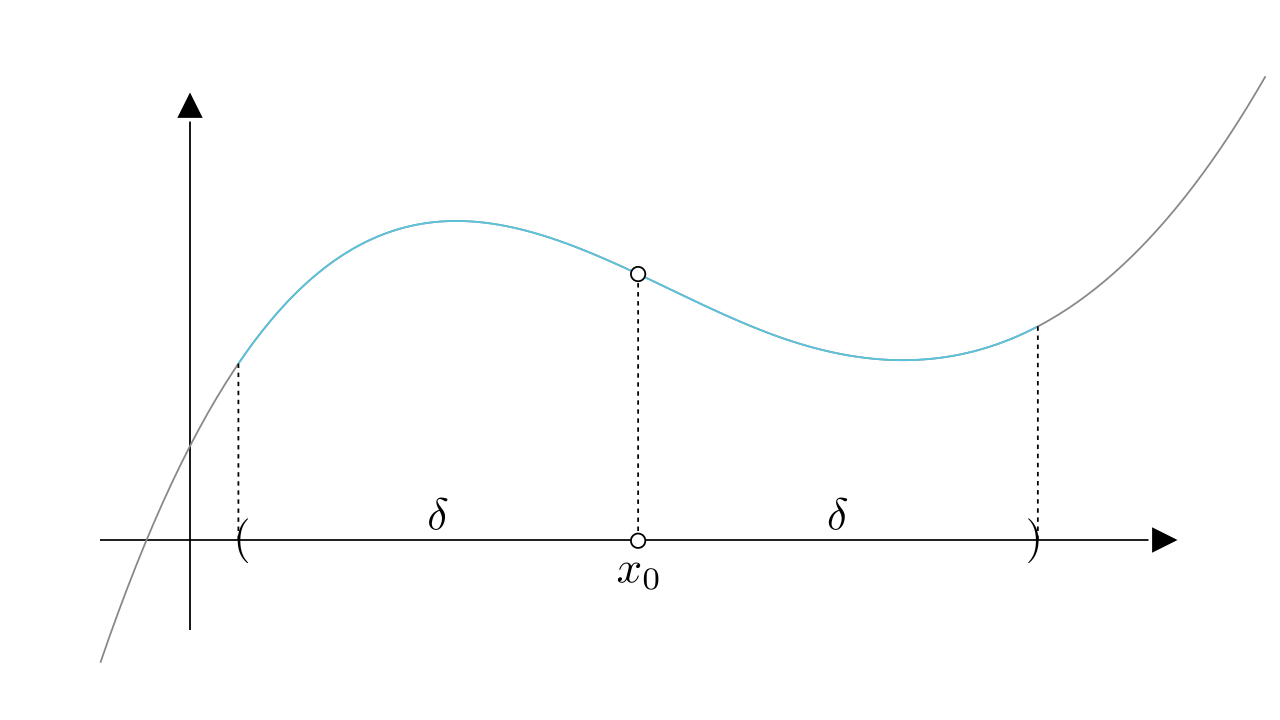
说起极限，大家都有画面感，比如我们要求图像在处的极限：

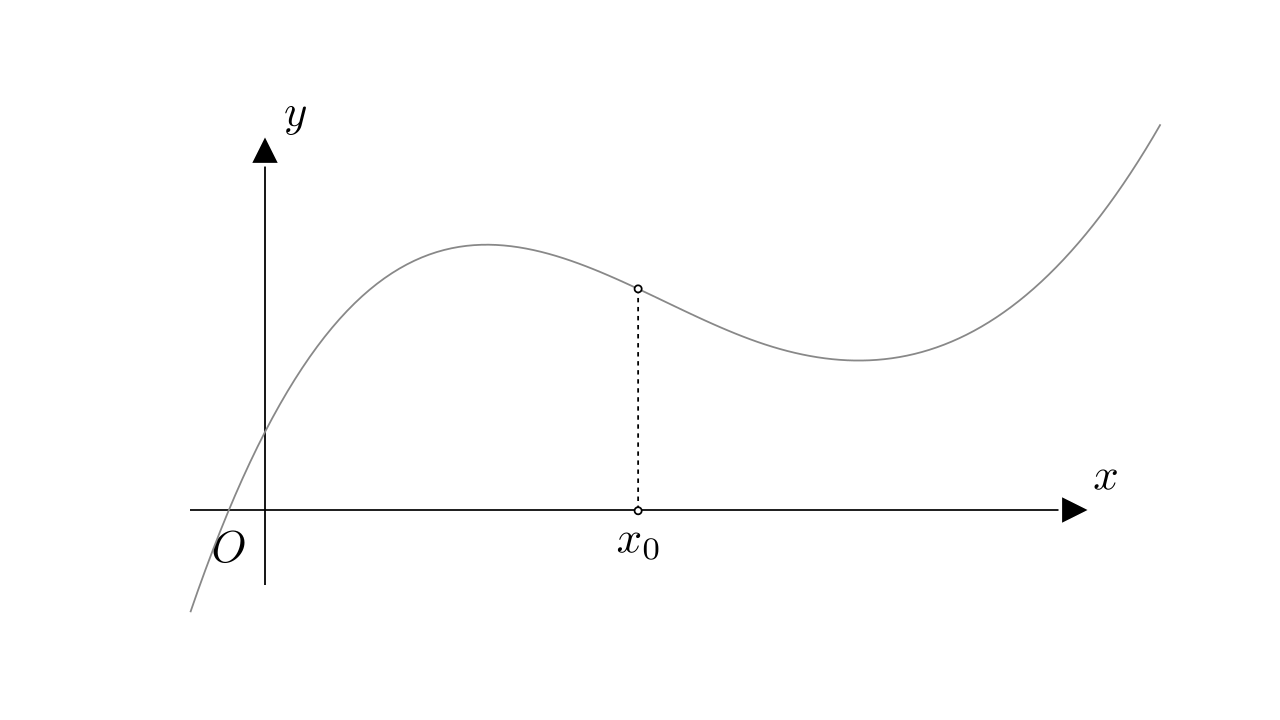
假如自变量无限接近，函数值无限接近一个确定的实数，那么这个确定的实数，就是函数的极限

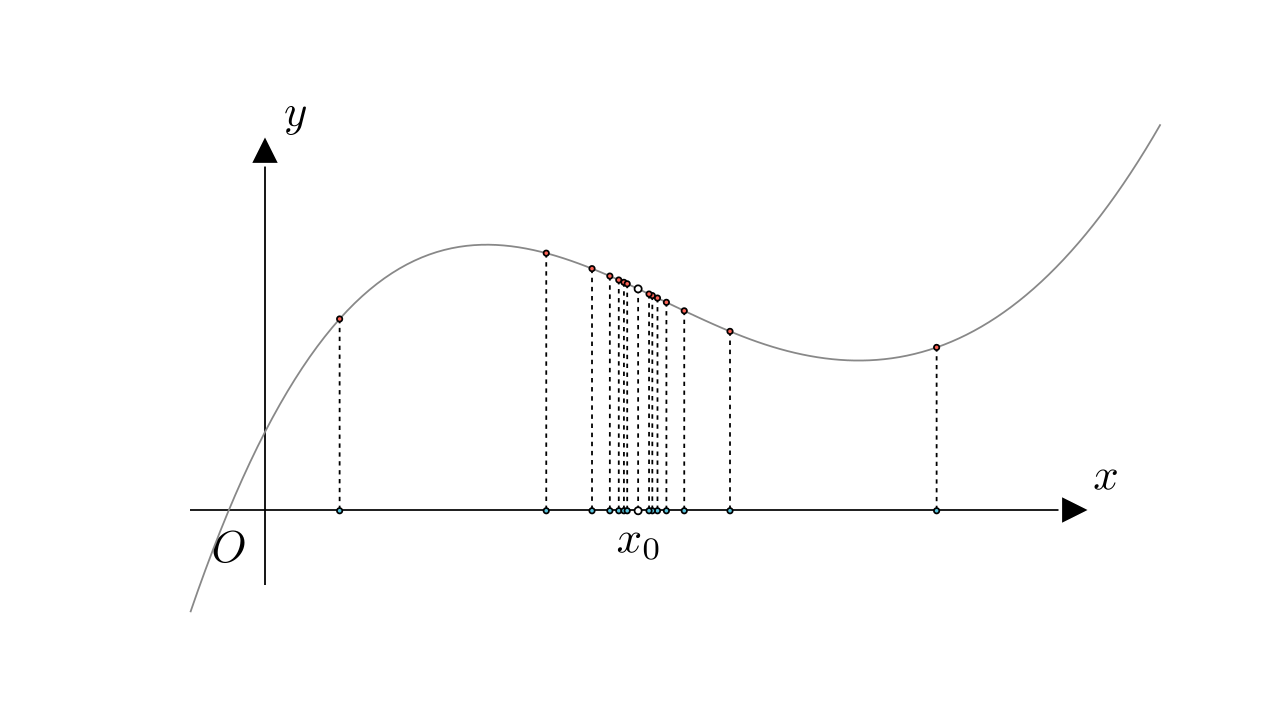
关键是如何定义什么叫无限接近，在这个视角下，我们觉得足够接近了

我们可以将它放大，还可以继续加点：

究竟怎样才算无限接近呢？这个问题困扰了数学家很长时间，最后由德国数学家，现代分析之父魏尔斯特拉斯给出了定义。

这定义内容看着挺多的，其实重要的就是前面两句：

如果这两句都满足，极限就存在。那么它们在说什么呢？我们来看一下

首先看，这里面有一个符号，它出现了两次，一次被记作，一次被记作,它们都被称为的去心邻域，什么意思呢？

我们以为中心，作出一段区域，这个区域被称为的邻域，记作，如果关心邻域的半径，也可以将这段区域记作

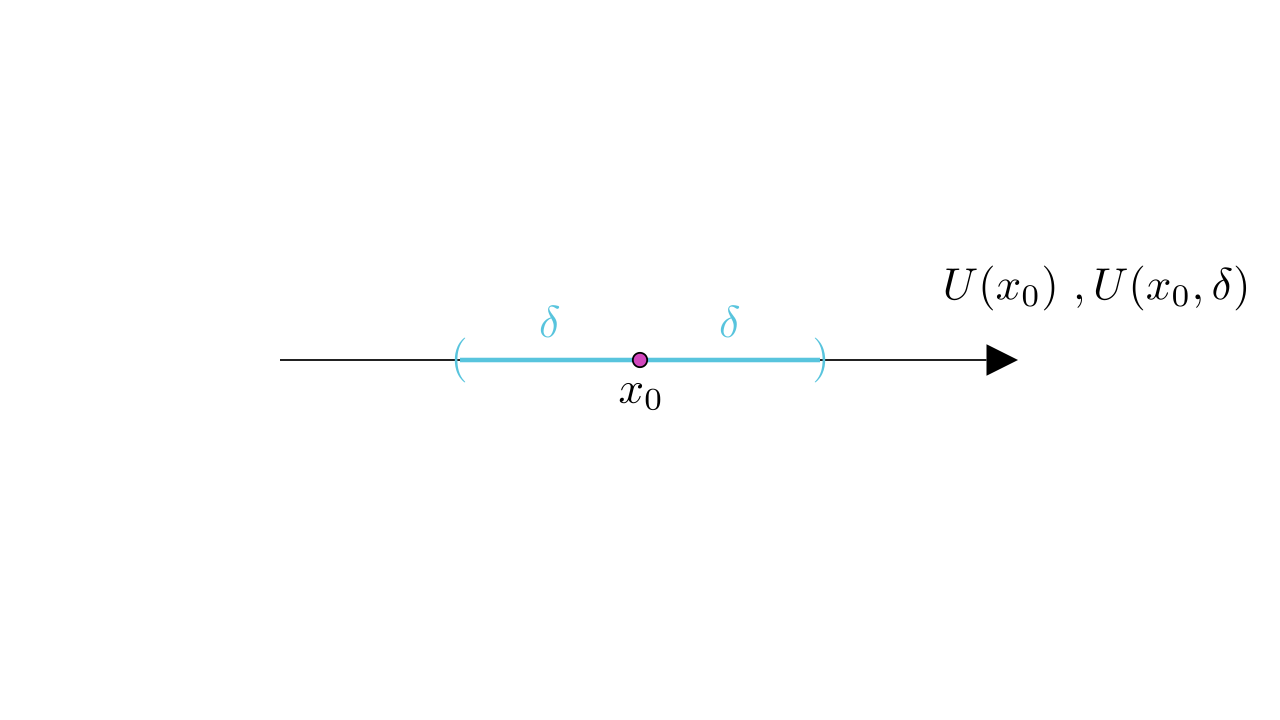
其它条件保持不变，去心邻域就是在邻域的基础上，拿掉这个点，此时被记作

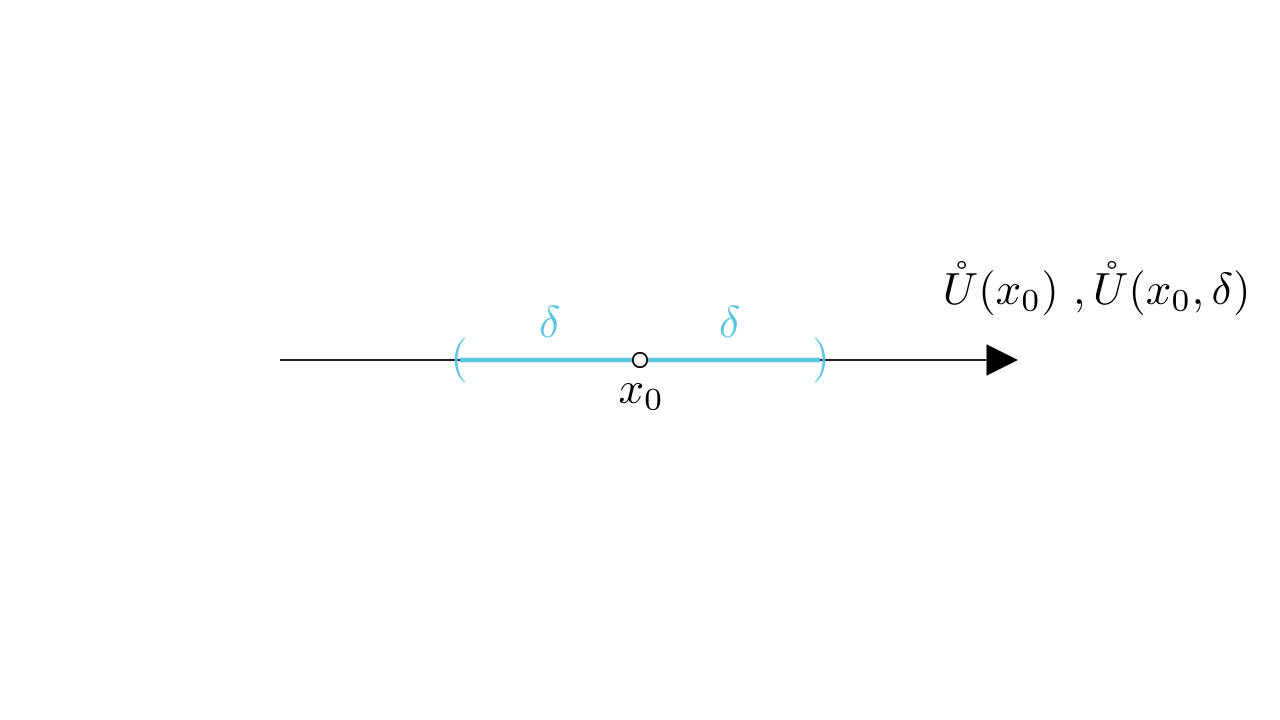
这两句话中还有两个变量,和,其中是去心邻域的半径，根据描述，函数在上有定义

而函数与极限距离的满足

因此是函数与极限距离的上限，要将它表示出来，我们可以以为中心，为半径，作出一个区域,显然，此区域内的点都满足：

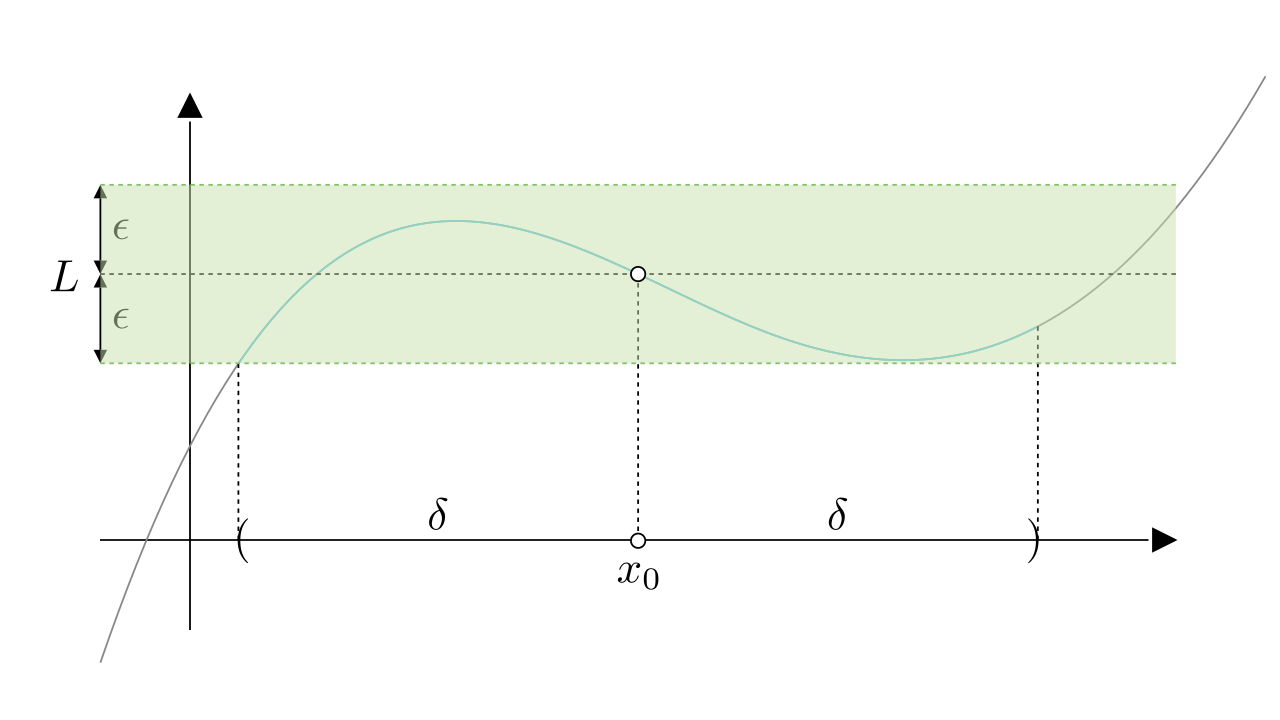
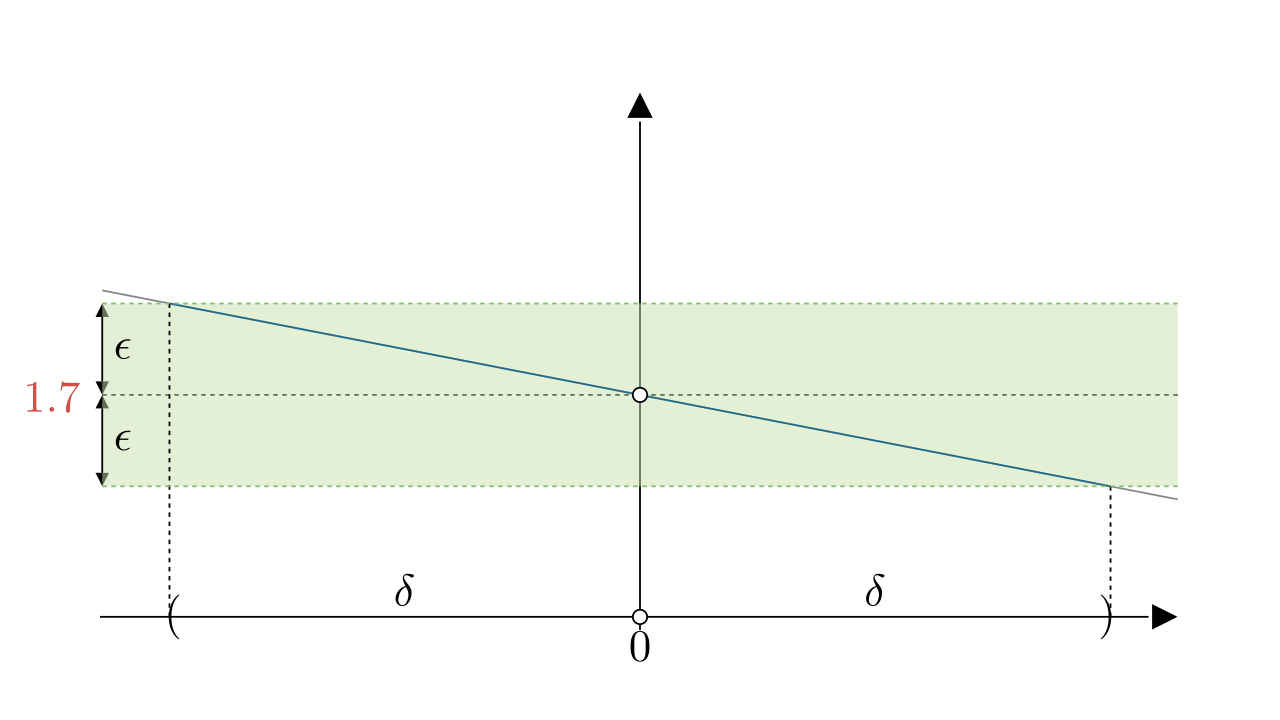
现在我们将定义中的变量、符号都翻译了一下，画出了上面这个图像，那是不是它就可以反应出函数极限的概念了呢？当然不是，我们还要将几句话连在一起进行理解。

这句话中最重要的就是对任意，存在，就是任意一个，都能找到对应的，使去心邻域内的函数都满足

从图中可以看到，随着变小，我们总能找到合适的，使得去心邻域内的图像都在区域内。因此极限为，记作：

定义介绍完了，下面我们来看一道具体的例题熟悉一下：

例：已知，求

先画出图像

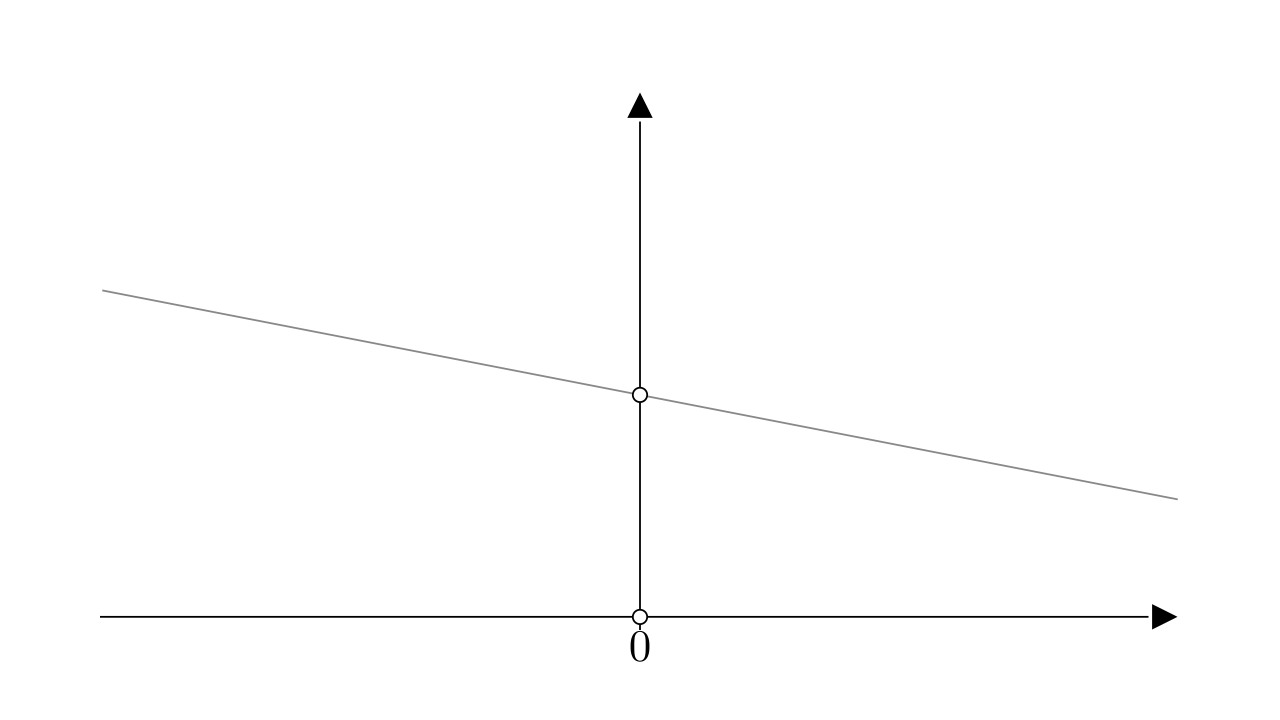
根据定义，如果极限为，那么对于任意的，都能找到满足：

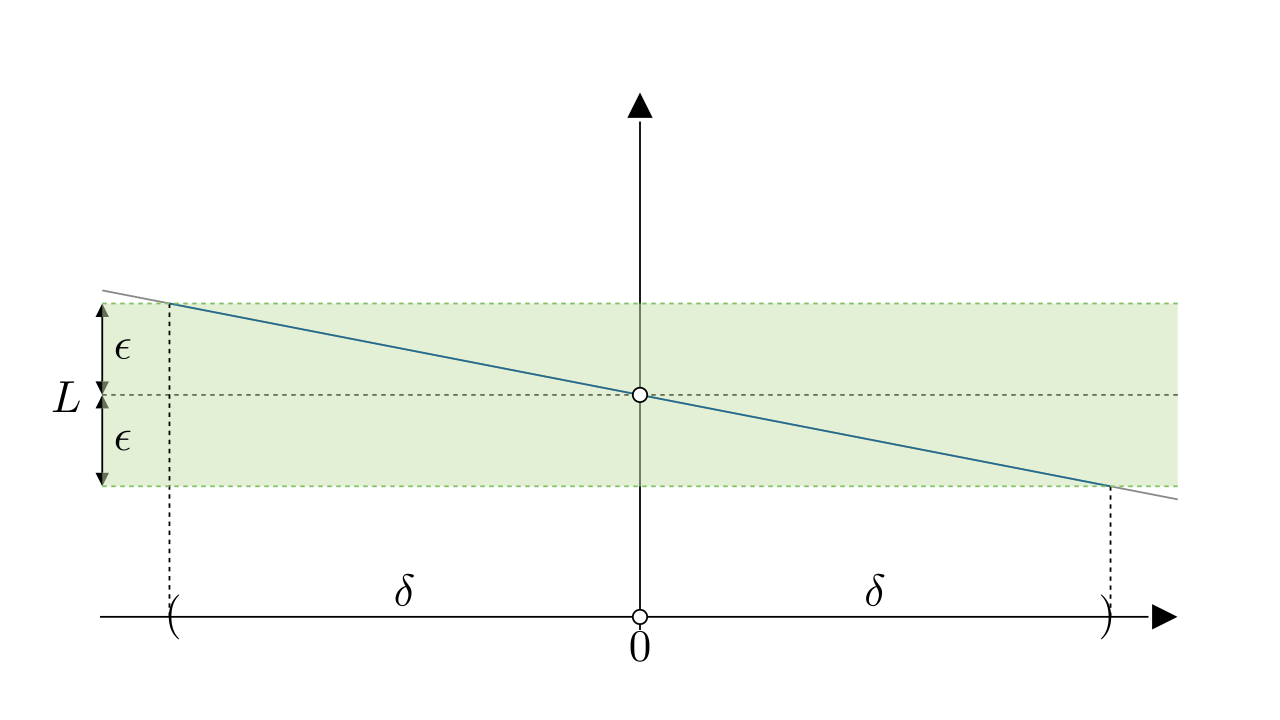
第一步，我们要猜测是多少，方法就是计算趋于0时，函数值趋于哪个值，我们取几个点计算，结果如下：

从结果，我们可以推测，极限值

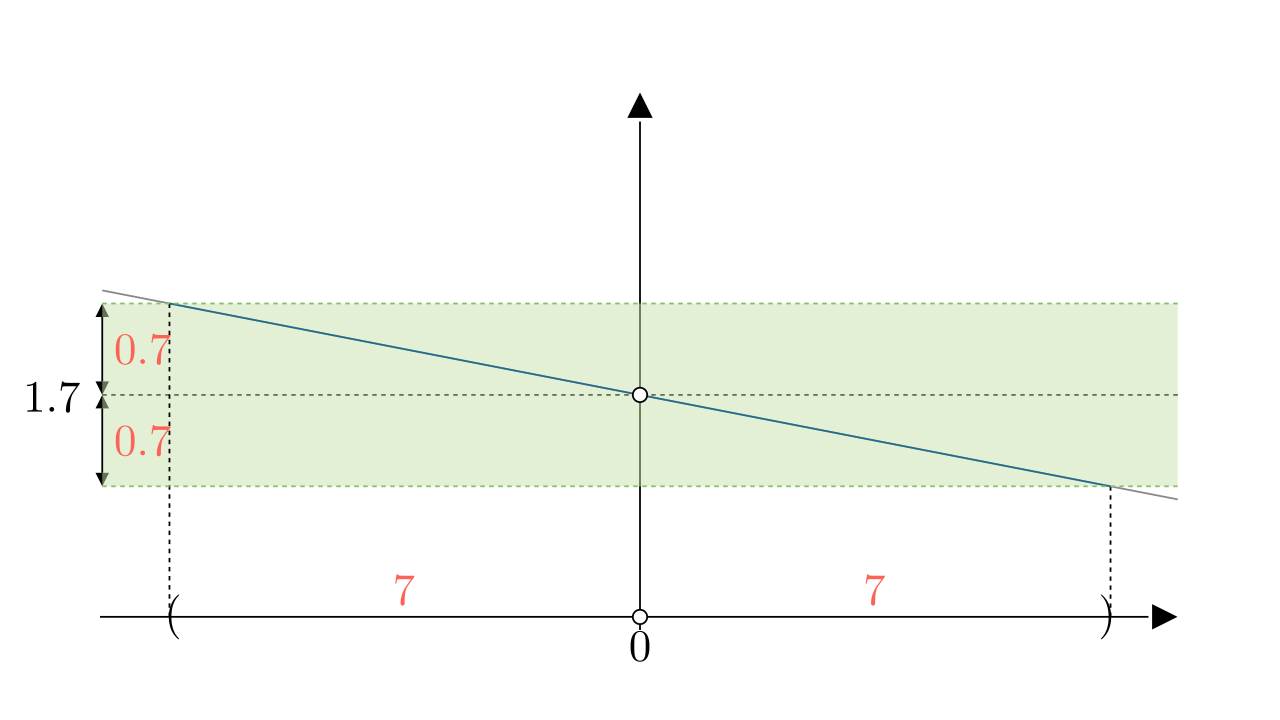
下面我们来进行验证：随便取一个，比如

解得：

即时，都满足，如图所示：

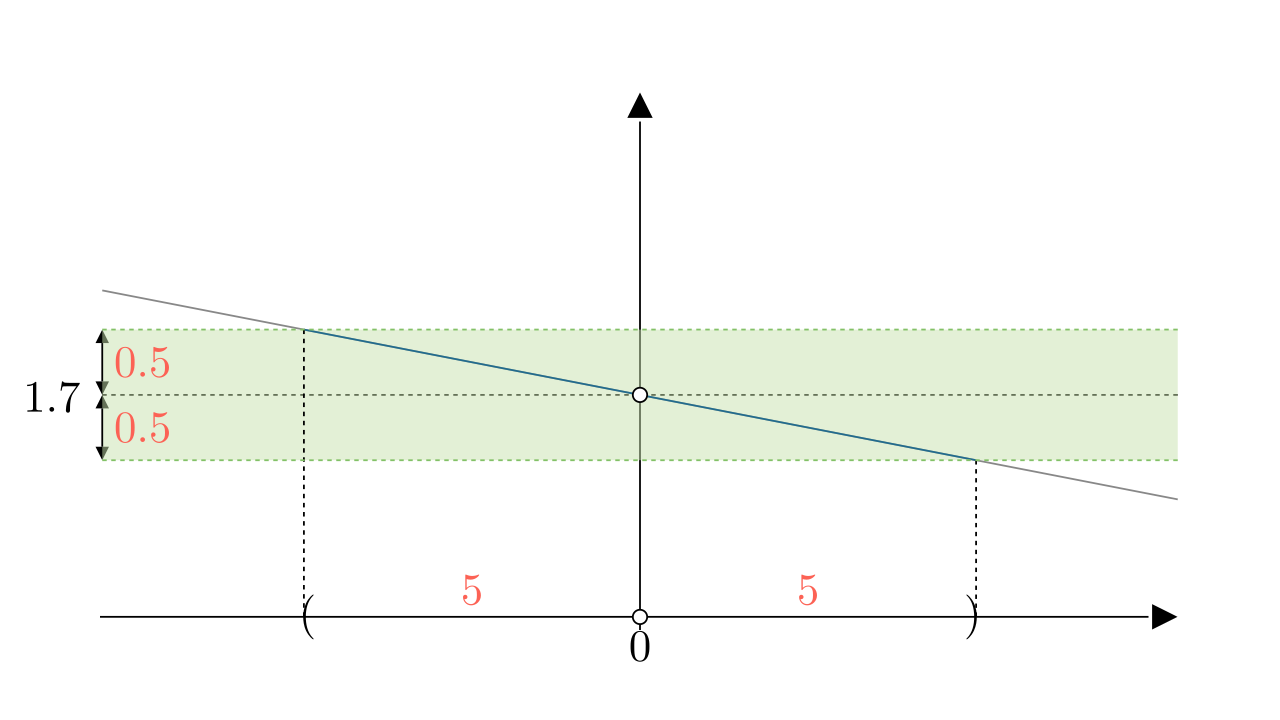
再取一个

同样可以得到时，都满足，如图所示：

对于任意，解不等式：

可以得到：

即时，都满足,因此极限为

例：已知，求

解：设极限为

因此取，使得满足

得到：