如何理解多变量函数的极限？

马同学

如何理解多变量函数的极限？

多变量函数的极限是单变量函数极限的扩展，让我们从数列极限的直观开始学习。

1 数列极限的直观

在古希腊的时候，人们就知道可以用等边多边形的面积来逼近圆形的面积：

假设用 $a_n$ 来表示内接等边 $n$ 边形的面积，那么可以用一个数列来描述这个逼近过程：

这个数列的极限就是圆形的面积：

$圆的面积=\lim_{n\to\infty}a_n$

可以通过直角坐标系中的图像来展示该数列极限，可以看到随着 $n$ 的增加，数列越来越逼近圆形的面积：

数列极限在《单变量微积分》有详细讲解，这里只是提下梗概。

2 函数极限的直观

2.1 单变量函数的极限

对于更一般的单变量函数的极限（数列可以看作是定义域为自然数的函数）：

$\lim_{x\to x_0}f(x)=L,\quad x\in\mathbb{R}$

如果将 $x\to x_0$ 看作，在 $x_0$ 的去心邻域内，从左侧或右侧逼近 $x_0$ 的点列：

那么极限 $\displaystyle\lim_{x\to x_0}f(x)=L$ 可以解读为，当 $x$ 沿着上述的点列逼近 $x_0$ 时，对应的函数值 $f(x)$ 也不断逼近 $L$ ：

2.2 多变量函数的极限

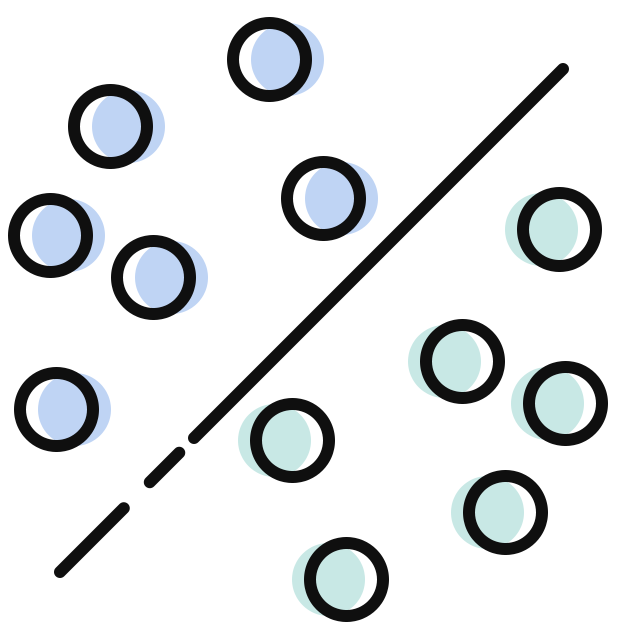
这种观点是可以推广到多变量函数的极限上去的，比如二元函数的极限：

$\lim_{(x,y)\to(x_0,y_0)}f(x,y)=L$

其中的 $(x,y)\to(x_0,y_0)$ 可以看作，在 $(x_0,y_0)$ 的去心邻域内，从四面八方逼近 $(x_0,y_0)$ 的点：

那么二元函数的极限就是，当 $(x,y)$ 沿着上述的点逼近 $(x_0,y_0)$ 时，对应的函数值 $f(x,y)$ 也不断逼近 $L$ （下图如果把 $L$ 画出来就太乱了，不过还是可以看出，沿着这些点，对应的函数值都逼近于同一个值）：

3 一元函数极限的定义

虽然直观看上去极限并不难理解，但由于数学上的原因（这在课程《单变量微积分》中解释过了，这里不再赘述），一元函数极限的严格定义并不简单。

3.1 一元函数极限的严格定义

设函数 $f(x)$ 在 $\mathring{U}(x_0)$ 上有定义。如果存在常数 $L$ ，对任意给定的正数 $\epsilon$ ，总存在正数 $\delta$ ，使得当 $x$ 满足不等式时（也就是 $x$ 属于 $x_0$ 的去心邻域）：

$0 < |x - x_0| < \delta$

对应的函数值 $f(x)$ 都满足不等式：

$|f(x) - L| < \epsilon$

那么常数 $L$ 就叫做函数 $f(x)$ 当 $x\to x_0$ 的极限，记作：

$\lim_{x\to x_0}f(x)=L\quad 或\quad f(x)\to L\ ( x\to x_0)$

这个定义在这里简单解释一下，如果函数 $f(x)$ 在 $x_0$ 点的极限为 $L$ ：

那么以 $L$ 为中心， $\epsilon$ 为半径构建一个区间 $(L-\epsilon,L+\epsilon)$ （下图用矩形来表示该区间），必能找到某正数 $\delta$ ，使得去心邻域 $\mathring{U}(x_0,\delta)$ 内的函数值都在该区间内（蓝色表示区间内的函数曲线，红色表示区间外的函数曲线）：

并且不论 $\epsilon$ 如何缩小，总能找到新的正数 $\delta$ ，使得去心邻域 $\mathring{U}(x_0,\delta)$ 内的函数值都在该区间内（下面动画展现了先缩小 $\epsilon$ ，然后寻找 $\delta$ 这个过程）：

如果满足上面所说的，那么有：

$\lim_{x\to x_0}f(x)=L$

3.2 回归直观

如果把每次找到的 $\mathring{U}(x_0,\delta)$ 的边界点保留下来：

沿着这些点列靠近 $x_0$ ，对应的函数值就会不断逼近 $L$ ，这又回到了之前我们对极限的直观上了：

4 聚点

二元函数的极限定义和一元函数类似，只是由于二元函数的邻域更复杂，所以需要引入聚点的概念：

如果对于任意给定的 $\delta > 0$ ，点 $P$ 的去心邻域 $\mathring{U}(P,\delta)$ 内总有平面点集 $E$ 中的点，那么称点 $P$ 为 $E$ 的 $\color{Salmon}{聚点}$ 。

比如下面的点 $P_0$ 就是一个聚点，随便怎么缩小它的去心领域的半径，去心邻域内总有平面点集 $E$ 中的点：

定义聚点是为了保证，从 $P_0(x_0,y_0)$ 的某去心邻域内的某一点 $P(x,y)$ 出发，至少能找到一串完全在 $E$ 中的点来靠近 $P_0$ ：

也就是说，聚点保证了下面这个极限过程是可行的、是存在的：

$P\to P_0\quad或\quad (x,y)\to(x_0,y_0)$

5 二元函数极限的定义

弄清楚聚点之后，下面可以给出二元函数极限的定义了：

设二元函数 $f(x,y)$ 的定义域为 $D$ ， $P_0(x_0,y_0)$ 是 $D$ 的聚点。如果存在常数 $L$ ，对于任意给定的正数 $\epsilon$ ，总存在正数 $\delta$ ，使得当点 $P(x,y)$ 满足下列条件时：

$(x,y)\in D\cap \mathring{U}(P_0,\delta)$

都有：

$|f(x,y)-L| < \epsilon$

成立，那么就称常数 $L$ 为函数 $f(x,y)$ 当 $(x,y)\to(x_0,y_0)$ 时的极限，记作：

$\lim_{(x,y)\to(x_0,y_0)}f(x,y)=L\quad 或\quad f(x,y)\to L\ \big(\ (x,y)\to(x_0,y_0)\ \big)$

因为这是二元函数的极限，所以也称作 $\color{Salmon}{二重极限}$ 。

5.1 与一元函数极限的区别

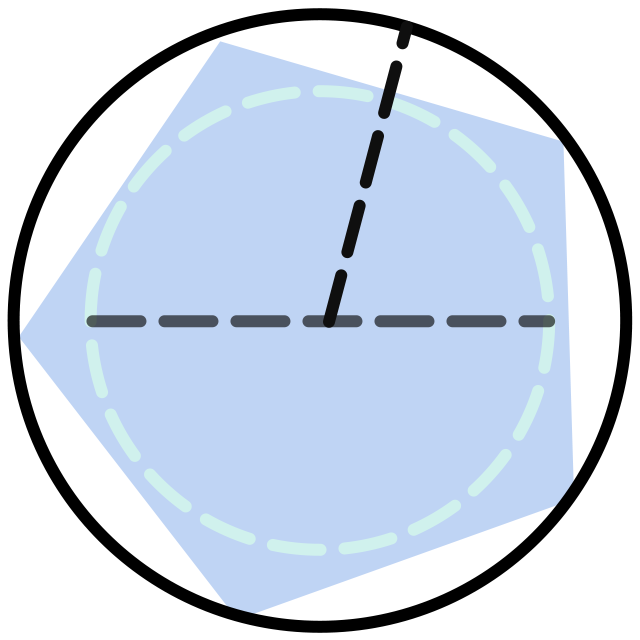
二重极限和一元函数极限定义相比，最大的区别在于：

$\begin{array}{c|c} \hline \quad 一次函数的极限 \quad&\quad 二次函数的极限\quad\\ \hline \\ \quad 函数f(x)在\mathring{U}(x_0)上有定义\quad&\quad 二元函数f(x,y)的定义域为D \quad \\ \quad 0 < |x - x_0| < \delta \quad&\quad (x,y)\in D\cap \mathring{U}(P_0,\delta) \quad\\ \\ \hline \end{array}$

在一元函数中，函数的定义域和去心邻域合二为一。而在二元函数中，函数的定义域 $D$ 和去心邻域 $\mathring{U}(P_0,\delta)$ 不一定重合，相交部分才是我们关心的：

并且 $P_0(x_0,y_0)$ 是 $D$ 的聚点，这样可以保证无论 $\delta$ 多小，去心邻域和定义域 $D$ 总是有相交部分的（当然也保证了能有一串靠近 $P_0(x_0,y_0)$ 的点）：

剩下的部分就和一元函数极限的定义差不多了。

5.2 二重极限定义的几何意义

假设二元函数 $f(x,y)$ 在 $P_0(x_0,y_0)$ 有极限 $L$ ：

那么以 $L$ 为中心， $\epsilon$ 为半径构建一个区间 $(L-\epsilon,L+\epsilon)$ ，必能找到某正数 $\delta$ ，使得符合下面条件的点：

$(x,y)\in D\cap \mathring{U}(P_0,\delta)$

对应的函数值都在该区间内：

当然，同一元函数的极限相同，随着 $\epsilon$ 的缩小，始终能够找到合适的 $\delta$ ，使得对应的函数值都在 $\epsilon$ 规定的区间内。并且这个过程意味着可以找到一串不断逼近 $P_0(x_0,y_0)$ 的点，沿着这串点，函数值不断逼近 $L$ ，最终可以得到：

$\lim_{(x,y)\to(x_0,y_0)}f(x,y)=L$

关注马同学